Gregory Newton Forward Interpolation Formula

Understanding and Application:

The Gregory Newton Forward Interpolation Formula is an important formula in the field of numerical analysis and interpolation techniques. This approach, which bears the names of its developers, James Gregory and Isaac Newton, is a potent tool for estimating a function’s values between known data points. It is part of the Newton’s divided difference interpolation formula family, which is intended to calculate values at positions between the supplied data points.

Understanding Interpolation:

In mathematics and computer science, interpolation is a fundamental idea, particularly when estimating unknown values from a set of known values. Consider a situation in which a set of data points at predetermined intervals represent a function. We can create a function that goes through these places precisely or estimate values at points that are in between using interpolation techniques. This is especially helpful in fields like computer graphics, engineering, statistics, and numerical analysis.

Origins and Development
:

The groundbreaking efforts of mathematicians and scientists who looked for effective ways to compute values between supplied data points are responsible for the creation of the Gregory Newton Forward Interpolation Formula. One of the greatest mathematicians of all time, Isaac Newton, established the concepts behind interpolation, providing the foundation for a variety of interpolation methods. The formulation that bears their names is the result of the major improvement and application of these approaches by the Scottish mathematician and astronomer James Gregory.

Formula Derivation
:

Newton’s divided difference formula, which iteratively computes coefficients based on the differences of function values at the provided data points, is the source of the Gregory Newton Forward Interpolation Formula. Values at places directly to the right of the data points are computed by the forward interpolation. Now let’s explore the formulation:

Given a set of n+1 data points (x₀ , y₀₎ , (x₁ , y₁), …, (x_n , y_n ) where x₀ < x₁ <..…< x_n .The following formula can be used to find the interpolated value y(x)  at a given point x inside the interval [x₀ , x_n]: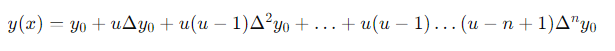
where

 u = x – x₀ / h

 h = x₁ − x₀

Δy₀ = y₁ – y₀ , Δy₀² ​= Δy₁ ​– Δy₀ and so on, are the forward differences.

Using the differences Δy_i , this recursive method effectively computes the value y(x), expanding the use of polynomial interpolation to forecast values beyond the provided data points.

Practical Application

The Gregory Newton Forward Interpolation Formula is used in many different fields where it is necessary to estimate or anticipate values between data points. Among the useful applications are:

Physics and Engineering

Interpolation aids in modeling complex systems and behavior prediction in engineering fields including civil, mechanical, and electrical engineering, where exact computations based on actual data are essential.

Financial Modeling

Interpolation techniques help smooth data and make projections between known financial indicators in the fields of finance and economics, where trends and forecasts are based on past data points.

Computer Animation and Graphics

Interpolation is a key component of computer graphics that ensures realistic movements and effects by displaying smooth animations and transitions between frames.

Scientific Investigation

Interpolation makes it easier to analyze trends and patterns in data in scientific study, especially in the experimental sciences where data points are collected from trials.

Advantages and limitations

Advantages

Simplicity:

It is easy to use and comprehend the formula.

Efficiency:

It offers a rapid approach to value estimation without requiring a lot of calculation.

Flexibility:

 It can be used with many kinds of data sets and functions.

   Limitations

Accuracy:

The degree of the interpolating polynomial and the distance between the data points determine accuracy.

Extrapolation:

Predicting values outside the range of the provided data points is not appropriate for this method.

Conclusion:

The inventiveness and contributions to mathematics of James Gregory and Isaac Newton are exemplified by the Gregory Newton Forward Interpolation Formula. Its usefulness in a variety of fields highlights the significance of this technique in contemporary computing techniques. Interpolation techniques continue to develop as processing power and technology grow, providing more accurate and effective means of interpreting and analyzing data.

Ultimately, the Gregory Newton Forward Interpolation Formula continues to be a fundamental tool in numerical analysis because it offers a strong framework for estimating values between known data points. This helps us better understand and model complex systems in science, engineering, and other fields.

Question:

From the following data find y at x = 43 using Newton forward interpolation formula.

x	40	50	60	70	80	90
y	184	204	226	250	176	304

 

From the following data find y at x = 43 using Newton forward interpolation formula.

x	40	50	60	70	80	90
y	184	204	226	250	176	304

Solution:

                 p = (x – x₀ ) / h

                         = (43 – 40) / 10

       p = 0.3

x	y	Δ1	Δ2	Δ3	Δ4	Δ5
40	184
		20 = 1y0
50	204		2 = ∆2y0
		22 = ∆1y1		0 = ∆3y0
60	226		2 = ∆2y1		-100 = ∆4y0
		24 = ∆1y2		-100 = ∆3y1		500 = ∆5y0
70	250		-98 = ∆2y2		400 = ∆4y1
		-74 = ∆1y3		300 = ∆3y2
80	176		202 = ∆2y3
		128 = ∆1y4
90	304

y_p = y₀ + p¹y₀ + p (p – 1) / 2 ²y₀ + p (p – 1) (p – 2) / 3 ³y₀ + p (p – 1) (p – 2) (p – 3) / 4 ⁴y₀ + p (p – 1) (p – 2)  (p – 3) (p – 4) / 5 ⁵y₀

 

     = 184 + 0.3 (20) + 0.3 (0.3 – 1) (2) / 2 + 0.3 (0.3 – 1) (0.3 – 2) (0) / 3 + 0.3 (0.3 – 1) (0.3 – 2) (0.3 – 3) (-100) / 4 × 3 × 2 ×1 + 0.3 (0.3 – 1) (0.3 – 2) (0.3 – 3)  ( 0.3 – 4) / 5 × 4 × 3 × 2 × 1

 

     = 184 + 6 + (-0.21) + 0 + 4.01625 + 14.860125

 

y_p = 208.666375

x	y	Δ1	Δ2	Δ3	Δ5	Δ6
40	184
		20 = 1y0
50	204		2 = ∆2y0
		22 = ∆1y1		0 = ∆3y0
60	226		2 = ∆2y1		-100 = ∆4y0
		24 = ∆1y2		-100 = ∆3y1		500 = ∆5y0
70	250		-98 = ∆2y2		400 = ∆4y1
		-74 = ∆1y3		300 = ∆3y2
80	176		202 = ∆2y3
		128 = ∆1y4
90	304

y_p = y₀ + p¹y₀ + p (p – 1) / 2 ²y₀ + p (p – 1) (p – 2) / 3 ³y₀ + p (p – 1) (p – 2) (p – 3) / 4 ⁴y₀ + p (p – 1) (p – 2)  (p – 3) (p – 4) / 5 ⁵y₀

 

     = 184 + 0.3 (20) + 0.3 (0.3 – 1) (2) / 2 + 0.3 (0.3 – 1) (0.3 – 2) (0) / 3 + 0.3 (0.3 – 1) (0.3 – 2) (0.3 – 3) (-100) / 4 × 3 × 2 ×1 + 0.3 (0.3 – 1) (0.3 – 2) (0.3 – 3)  ( 0.3 – 4) / 5 × 4 × 3 × 2 × 1

 

     = 184 + 6 + (-0.21) + 0 + 4.01625 + 14.860125

 

y_p = 208.666375

Question:

The population of a town in decennial census was as given below. Estimate the population for the year 1895.

Years (x)	1891	1901	1911	1921	1931
Population (y) in thousands	46	66	81	93	101

 

The population of a town in decennial census was as given below. Estimate the population for the year 1895.

Years (x)	1891	1901	1911	1921	1931
Population (y) in thousands	46	66	81	93	101

 

Solution:

     

p = x – x₀ / h

          = 1895 – 1891 / 10

p = 0.4

x	y	Δ1	Δ2	Δ3	Δ4
1891	46
		20 = Δ1y0
1901	66		-5 = ∆2y0
		15 = ∆1y1		2 = ∆3y0
1911	81		-3 = ∆2y1		-3 = ∆4y0
		12 = ∆1y2		-1 = ∆3y1
1921	93		-4 = ∆2y2
		8 = ∆1y3
1931	101

 

y_p = y₀ + p¹y₀ + p (p – 1) / 2 ²y₀ + p (p – 1) (p – 2) / 3 ³y₀ + p (p – 1) (p – 2) (p – 3) / 4 ⁴y₀

 

    = 46 + 0.4 (20) + 0.4 (0.4 – 1) (-5) / 2 + 0.4 (0.4 – 1) (0.4 – 2) (2) / 6 + 0.4 (0.4 – 1) (0.4 – 2) (0.4 – 3) (-3) / 4 × 3 × 2 ×1

 

    = 46 + 8 + 0.6 + 0.128 + 0.1248

 

y_p = 54.8528

x	y	Δ1	Δ2	Δ3	Δ4
1891	46
		20 = Δ1y0
1901	66		-5 = ∆2y0
		15 = ∆1y1		2 = ∆3y0
1911	81		-3 = ∆2y1		-3 = ∆4y0
		12 = ∆1y2		-1 = ∆3y1
1921	93		-4 = ∆2y2
		8 = ∆1y3
1931	101

 

y_p = y₀ + p¹y₀ + p (p – 1) / 2 ²y₀ + p (p – 1) (p – 2) / 3 ³y₀ + p (p – 1) (p – 2) (p – 3) / 4 ⁴y₀

 

    = 46 + 0.4 (20) + 0.4 (0.4 – 1) (-5) / 2 + 0.4 (0.4 – 1) (0.4 – 2) (2) / 6 + 0.4 (0.4 – 1) (0.4 – 2) (0.4 – 3) (-3) / 4 × 3 × 2 ×1

 

    = 46 + 8 + 0.6 + 0.128 + 0.1248

 

y_p = 54.8528

Frequently Asked Questions (FAQs):

Q) What is the Gregory Newton Forward Interpolation Formula?

A technique to approximate function values between known data points is the Gregory Newton Forward Interpolation Formula. This formula, which is part of Newton’s split difference interpolation formulas, is intended to calculate values at points that are situated to the right of the provided data points.

Q) Who developed the Gregory Newton Forward Interpolation Formula?

James Gregory and Isaac Newton, who made substantial contributions to the advancement of mathematical interpolation methods, are honored in the formula’s namesake. They improved and codified the ideas underlying Newton’s split difference technique.

Q) How does the formula differ from other interpolation methods?

One of Newton’s split difference formulae, which covers both forward and backward interpolation techniques, is the Gregory Newton Forward Interpolation Formula. Values are computed using the forward and backward methods, respectively, to the right and left of the data points.

Q) What are the practical applications of the Gregory Newton Forward Interpolation Formula?

Applications for this method can be found in many different domains, including science research (for evaluating experimental data), computer graphics (for smooth animations), finance (for trend predictions), and engineering (for numerical analysis and modeling).

Q) What are the advantages of using the Gregory Newton Forward Interpolation Formula?

The formula offers a rapid way to estimate values between known data points and is rather easy to use and comprehend. It is adaptable and suitable for a variety of functions and data sets.

Q) Are there any limitations to the Gregory Newton Forward Interpolation Formula?

Indeed, although it works well for interpolation within the specified data point range, it might not be able to anticipate values outside of this range with enough accuracy (extrapolation). The distribution and spacing of the data points also affect accuracy.

Q) How is the Gregory Newton Forward Interpolation Formula calculated?

Recursively calculating coefficients based on forward differences of function values at the specified data points is required to solve the formula. In order to approximate values at in-between points between the known data points, it employs a polynomial interpolation technique.

Q) Can the Gregory Newton Forward Interpolation Formula handle non-equidistant data points?

As long as the data points are arranged according to their x-values in ascending order, the algorithm is capable of handling non-equidistant data points. To reliably interpolate numbers, it computes differences based on the time interval between successive data points.

Q) What are some alternatives to the Gregory Newton Forward Interpolation Formula?

Other interpolation techniques including Lagrange interpolation, Hermite interpolation, cubic spline interpolation, and Neville’s algorithm are alternatives. The particulars of the problem and the type of data determine which approach is best.

Q) Where can I learn more about implementing the Gregory Newton Forward Interpolation Formula?

Comprehensive explanations and examples of applying the formula in many contexts can be found in resources including research papers on interpolation techniques, online courses on numerical analysis, and textbooks on numerical methods.