Gregory Newton Backward Interpolation Formula
Exploring the Techniques and Applications
The Gregory Newton Backward Interpolation Formula is a key tool in mathematical interpolation and numerical analysis for estimating values between known data points. This technique, which bears the names of its creators, James Gregory and Isaac Newton, is especially helpful when a function’s values are known at evenly spaced intervals but the desired interpolation point is located ahead of the last known data point.
Understanding Interpolation
The technique of guessing unknown values that fall between a ranges of known values is known as interpolation. This method is crucial for building approximations of functions based on discrete data points in numerical analysis. In particular, the Gregory Newton Backward Interpolation Formula takes care of situations in which a value needs to be estimated that come before the final known data point.
Historical Context and Development
:
The formula owes its beginnings to the key contributions of Sir Isaac Newton, whose foundational work in mathematics and calculus established the theoretical basis for interpolation techniques, and James Gregory, a Scottish mathematician noted for his work on infinite series and interpolation. This interpolation formula was made possible by Newton’s forward and backward difference methods, which expanded the range of applications for interpolation techniques beyond basic linear interpolation.
Mathematical Formulation
The following is an expression for the Gregory Newton Backward Interpolation Formula:
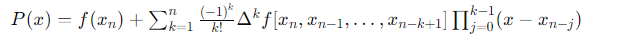
Where:
P(x) is the interpolated polynomial.
f(xn) are the function values at the equally spaced points xn.
Δkf [xn , xn-1,…, xn-k+1] denotes the backward finite differences of f.
Application and Usage
The formula is used in many disciplines, including as computer science, physics, engineering, and economics, where modeling and analysis need the interpolation of discrete data.
Financial Predictive Modeling:
In the finance industry, historical stock prices and economic data are frequently accessible at specific intervals of time. These data points can be estimated to have intermediate values using Gregory-Newton backward interpolation, which can subsequently be utilized to fill in missing data or in forecasting models.
Curve Fitting:
Backward interpolation can be used to fit a curve through experimental data points that are not regularly spaced. This is helpful in disciplines like engineering, chemistry, and physics where experimental data is gathered irregularly.
Signal Processing:
Discrete interval sampling of data points is a possible scenario in digital signal processing. Estimating values between these discrete samples can be facilitated by backward interpolation, which can help with filtering and signal reconstruction tasks.
Data compression:
To reduce the amount of data required to represent a signal or a picture while retaining a decent level of accuracy, data compression algorithms can make use of interpolation techniques such as Gregory-Newton backward interpolation.
Error Analysis:
By calculating the predicted values between measured points, interpolation techniques can assist in spotting outliers or inconsistencies in the data set while examining mistakes in experimental data or measurements.
Computer Graphics:
Interpolation is used in computer graphics and animation to produce seamless key frame transitions. Finding intermediate values for animation pathways or transitions can be aided by the use of backward interpolation.
Simulation and Modeling:
Backward interpolation can be used to forecast the behavior of the system between measured points in simulation and modeling of physical systems where continuous solutions based on discrete data points are required.
In conclusion, the Gregory-Newton backward interpolation formula is a useful tool for both theoretical research and real-world applications. It finds use in many different domains where values between known data points need to be estimated or predicted.
Computational Steps
To use the Backward Interpolation Formula for Gregory Newton:
Data Preparation:
Arrange known data points (xn , f(xn)) in ascending order of x.
Calculate Backward Differences:
Compute the backward differences Δkf [xn , xn-1,…, xn-k+1] iteratively using:
Δ1f [xn , xn-1] = f[xn] − f[xn-1]
Δ2f [xn , xn-1, xn-2] = Δ1f [xn , xn-1] – Δ1f [xn-1 , xn-2] and so forth.
Construct the Interpolating Polynomial:
Substitute the backward differences into the formula to obtain P(x).
Advantages and limitations
Advantages
Accuracy:
Based on established data points, this method produces accurate estimates for intermediate values.
Computational Efficiency:
Because backward differences are recursive, they make computations easier.
Limitations
Dependency on evenly Spaced Data:
Accurate interpolation necessitates evenly spaced data points.
Sensitivity to Noise:
A tendency to magnify data inaccuracies.
Practical Example
Consider a set of temperature readings over time:
(0, 20) , (1, 22) , (2, 25) , (3, 27) , (4, 30)
To estimate the temperature at t = −1:
Compute backward differences.
Apply the Gregory Newton Backward Interpolation Formula
Conclusion:
James Gregory and Isaac Newton’s mathematical genius and inventiveness are exemplified by the Gregory Newton Backward Interpolation Formula. It is a useful tool in both theoretical and practical applications across numerous fields because of its elegant ability to produce accurate predictions for values preceding existing data points. Such interpolation approaches will become increasingly relevant and useful in contemporary scientific and engineering activities as computing capabilities continue to advance.
Question:
The following data gives the melting point of an alloy of lead and zinc, where t is the temperature and p is the percentage of lead in the alloy.
|
p |
40 |
50 |
60 |
70 |
80 |
90 |
|
t |
184 |
204 |
226 |
250 |
276 |
304 |
Using newton backward interpolation formula find the melting point of alloy containing 84% of lead.
The following data gives the melting point of an alloy of lead and zinc, where t is the temperature and p is the percentage of lead in the alloy.
|
p |
40 |
50 |
60 |
70 |
80 |
90 |
|
t |
184 |
204 |
226 |
250 |
276 |
304 |
Using newton backward interpolation formula find the melting point of alloy containing 84% of lead.
Solution:
p = x – xn / h
= 84 – 90 / 10
p = – 0.6
|
x |
y |
∇1 |
∇2 |
∇3 |
∇4 |
∇5 |
|
40 |
184 |
|
|
|
|
|
|
|
|
20 = ∇1t1 |
|
|
|
|
|
50 |
204 |
|
2 = ∇2t2 |
|
|
|
|
|
|
22 = ∇1t2 |
|
0 = ∇3t3 |
|
|
|
60 |
226 |
|
2 = ∇2t3 |
|
0 = ∇4t4 |
|
|
|
|
24 = ∇1t3 |
|
0 = ∇3t4 |
|
0 = ∇5t5 |
|
70 |
250 |
|
2 = ∇2t4 |
|
0 = ∇4t5 |
|
|
|
|
26 = ∇1t4 |
|
0 = ∇3t5 |
|
|
|
80 |
276 |
|
2 = ∇2t5 |
|
|
|
|
|
|
28 = ∇1t5 |
|
|
|
|
|
90 |
304 |
|
|
|
|
|
yp = yn + p1yn + p (p +1) / 2 2yn + p (p + 1) (p + 2) / 3 3yn + p (p + 1) (p + 2) (p + 3) / 4 4yn + p (p + 1) (p + 2) (p + 3) (p + 4) / 5 5yn
= 304 + (-0.6) (28) + (-0.6) (-0.6 + 1) (2) / 2×1 + 0 + 0 + 0
= 304 – 16.8 – 0.24
yp = 286.96
yp = 287
|
x |
y |
∇1 |
∇2 |
∇3 |
∇4 |
∇5 |
|
40 |
184 |
|
|
|
|
|
|
|
|
20 = ∇1t1 |
|
|
|
|
|
50 |
204 |
|
2 = ∇2t2 |
|
|
|
|
|
|
22 = ∇1t2 |
|
0 = ∇3t3 |
|
|
|
60 |
226 |
|
2 = ∇2t3 |
|
0 = ∇4t4 |
|
|
|
|
24 = ∇1t3 |
|
0 = ∇3t4 |
|
0 = ∇5t5 |
|
70 |
250 |
|
2 = ∇2t4 |
|
0 = ∇4t5 |
|
|
|
|
26 = ∇1t4 |
|
0 = ∇3t5 |
|
|
|
80 |
276 |
|
2 = ∇2t5 |
|
|
|
|
|
|
28 = ∇1t5 |
|
|
|
|
|
90 |
304 |
|
|
|
|
|
yp = yn + p1yn + p (p +1) / 2 2yn + p (p + 1) (p + 2) / 3 3yn + p (p + 1) (p + 2) (p + 3) / 4 4yn + p (p + 1) (p + 2) (p + 3) (p + 4) / 5 5yn
= 304 + (-0.6) (28) + (-0.6) (-0.6 + 1) (2) / 2×1 + 0 + 0 + 0
= 304 – 16.8 – 0.24
yp = 286.96
yp = 287
Frequently Asked Questions (FAQs):
Q) What is the Gregory Newton Backward Interpolation Formula?
When the intended interpolation point lies ahead of the last known data point, a mathematical technique known as the Gregory Newton Backward Interpolation Formula can be used to estimate values between known data points. By employing backward finite differences, it expands the notion of interpolation beyond linear interpolation.
Q) Who developed the Gregory Newton Backward Interpolation Formula?
James Gregory and Sir Isaac Newton are honored in the formula’s names. The creation of both forward and backward difference approaches can be attributed to the work of Scottish mathematician James Gregory and the calculus-renowned scientist Isaac Newton.
Q) When is the Gregory Newton Backward Interpolation Formula used?
When one needs to estimate values that precede the last known data point and historical data is only accessible up to a specific point, this method comes in handy. It is used for modeling and analysis in many disciplines, including computer science, physics, engineering, and economics.
Q) How is the Gregory Newton Backward Interpolation Formula different from other interpolation methods?
The backward interpolation method estimates values prior to the final data point, in contrast to forward interpolation methods, which estimate values beyond the last known data point. This makes it appropriate for situations when future estimates are required and historical data is available.
Q) What are the advantages of using the Gregory Newton Backward Interpolation Formula?
- Accuracy:
Based on known data points, provides accurate estimates.
- Versatility:
Adaptable to different data sets with uniformly spaced values.
- Efficiency:
Because it is recursive and has backward differences, it is computationally efficient.
Q) How do you implement the Gregory Newton Backward Interpolation Formula in practice?
To apply the equation:
Sort the known data points according to x in ascending order.
Recursively calculate the backward differences.
To create the interpolating polynomial P(x), substitute the backward differences into the formula.
Q) Can the Gregory Newton Backward Interpolation Formula handle non-equally spaced data points?
No, for accurate interpolation, the formula requires that the data points be evenly spaced. Other interpolation techniques like Lagrange or spline interpolation can be more appropriate if the data points are not evenly spaced.
Q) In what fields is the Gregory Newton Backward Interpolation Formula commonly applied?
It is frequently used in computer science to optimize algorithms based on past performance data, in physics to predict values based on experimental data, in engineering to calculate trajectories, and in economics to forecast trends.
Q) What are some practical examples where the Gregory Newton Backward Interpolation Formula is useful?
Utilizing current weather data to estimate historical temperatures.
Forecasting past stock prices prior to the most recent data point that is accessible.
Utilizing the trajectory data of moving objects to compute their past positions.
