Gauss Backward Interpolation Formula
Introduction
In computer mathematics and numerical analysis, interpolation is a basic idea that involves estimating values within the range of a discrete collection of known data points. The Gauss backward interpolation algorithm is one of the most used interpolation techniques because it works well with data points that are equally spaced. This formula, which bears the name of the renowned mathematician Carl Friedrich Gauss, is very helpful for interpolating values near the conclusion of a data collection. The origin, uses, and benefits of the Gauss backward interpolation formula are explained in detail in this article.
Understanding Interpolation
It’s important to understand the fundamentals of interpolation before delving into the details of the Gauss backward interpolation formula. The goal of interpolation is to estimate unknown values by applying a function’s known values at particular places. The most basic type of interpolation, known as linear interpolation, approximates values between two known data points using a straight line. Higher-degree polynomials are used in more complex techniques, such as polynomial interpolation, to achieve higher accuracy.
Polynomial Interpolation and Gauss Interpolation Formulas
A polynomial is used in polynomial interpolation to iterate through a given set of data points. The Newton interpolation formula or the Lagrange interpolation formula is the generic form of polynomial interpolation. Although these techniques work well, they can become computationally demanding when dealing with big data sets. Gauss created interpolation algorithms especially for data points that were equally spaced in order to overcome these difficulties.
The Gauss forward interpolation formula and the Gauss backward interpolation formula are the two variations of the Gauss interpolation formula. While the latter is optimized for values at the conclusion of the data set, the former is used to estimate values near the beginning of the data set. The Gauss backward interpolation formula is the main topic of this article since it has special benefits under certain conditions.
Derivation of the Gauss Backward Interpolation Formula
Newton’s backward difference formula, which is designed for data points that are evenly spaced, is the source of the Gauss backward interpolation formula. The formula for Newton’s backward difference is as follows:
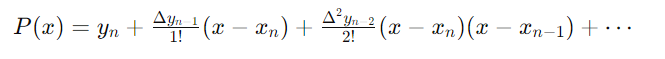
Here, yn represents the function’s value at the latest known data point, while Δ stands for the backward difference operator.
In order to increase precision and computing efficiency for points close to the end of the data set, Gauss changed this formula. The formula for Gauss backward interpolation is as follows: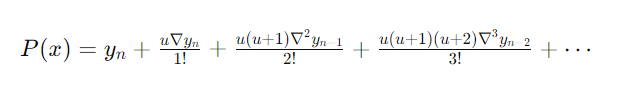
The backward difference operator is denoted by the symbol ∇ in this expression, and u = x – xn / h
where the distance between the data points is represented by h.
Applying the Gauss Backward Interpolation Formula
In order to demonstrate the use of the Gauss backward interpolation formula, let us have a look at a collection of data points that are evenly spaced: (x0 , y0 ), (x1 , y1 ),……, (xn , yn ) . Let’s say we have to calculate the function’s value at a location x that is close to xn.
Calculate Backward Differences:
The first step is to compute the backward differences of the data points. The first backward difference ∇yi is defined as:
∇yi = yi – yi-1
The second backward difference ∇2yi is:
∇2yi = ∇yi − ∇yi-1
Continue calculating higher-order backward differences as needed.
Determine u:
Compute the value of u using the formula u = x – xn / h
Substitute Values:
Substitute the known values of yn , ∇yn , ∇2yn-1 ,……, and u into the Gauss backward interpolation formula.
Compute the Interpolated Value:
Evaluate the polynomial to obtain the estimated value at the desired point x.
Advantages of the Gauss Backward Interpolation Formula
The Gauss backward interpolation formula is a useful technique in numerical analysis because it has the following benefits:
Accuracy Towards the End of the Data Set:
Compared to other methods, it offers a better degree of accuracy when estimating values towards the end of the data set.
Efficiency
The formula reduces processing complexity and is computationally efficient, particularly for data points that are evenly spaced.
Flexibility:
In situations when the function shows a great deal of variability, it can accommodate higher-order polynomials, enabling more accurate approximations.
Smooth Transitions:
The formula minimises sudden shifts that can happen with other interpolation methods by ensuring smooth transitions between known and interpolated values.
Limitations and Considerations
The Gauss backward interpolation formula has some drawbacks despite its benefits:
Evenly Spaced Data Requirement:
The formula is made to work only with data points that are evenly spaced. If the data are not evenly spaced, it might not function correctly.
Complexity for Large Data Sets:
Although this method is more efficient than others, it can still become complex for very large data sets, requiring high-order differences to be carefully computed.
Sensitivity to Errors:
Just like other polynomial interpolation techniques, this one has the potential to produce erroneous results if the input data is noisy or imprecise.
Conclusion:
When it comes to accurate and effective interpolation for equally spaced data points near the conclusion of the data set, the Gauss backward interpolation formula stands out as a potent weapon in the toolbox of numerical analysers. High accuracy and processing efficiency are ensured by its derivation from Newton’s backward difference formula and subsequent revisions by Gauss. Although it has some drawbacks, its benefits make it a priceless technique for particular interpolation situations. The Gauss backward interpolation method is an essential tool in scientific and engineering computations because it may greatly improve the precision and consistency of numerical approximations when applied correctly.
Frequently Asked Questions (FAQs):
Q) What is the Gauss backward interpolation formula?
A numerical technique for estimating the value of a function at a point close to the end of a given series of equally spaced data points is the Gauss backward interpolation formula. It is intended to offer excellent accuracy and computing efficiency, and it is developed from Newton’s backward difference formula.
Q) How does the Gauss backward interpolation formula differ from the Gauss forward interpolation formula?
While the Gauss backward interpolation formula is optimized for values towards the end of the data set, the Gauss forward interpolation formula is used to estimate values near the beginning of the data set. Although they are customised for distinct portions of the data set, both formulas are drawn from Newton’s difference formulas.
Q) What are the key components of the Gauss backward interpolation formula?
The key components include:
yn: The value of the function at the last known data point.
∇y: The backward difference operator.
u: A variable defined as x – xn / h , where h is the interval between data points.
Higher-order backward differences: ∇2y , ∇3y , etc.
Q) When should I use the Gauss backward interpolation formula?
When estimating the value of a function at the end of a collection of evenly spaced data points, use the Gauss backward interpolation formula. It is especially helpful in situations when precision close to the data set boundary is crucial.
Q) How do I compute the backward differences required for the formula?
To determine the backward differences:
The first backward difference is as follows:
∇yi = yi – yi-1
The second difference in reverse is:
∇2yi = ∇yi − ∇yi-1
If necessary, carry out same procedure for higher-order discrepancies.
Q) What is the formula for the Gauss backward interpolation?
The formula for Gauss backward interpolation is:
![]()
where u = x – xn / h
Q) Can the Gauss backward interpolation formula be used for irregularly spaced data points?
No, the formula for Gauss backward interpolation is intended only for data points that are equally spaced. If the data are not evenly spaced, it might not function correctly. Other interpolation techniques, such as Lagrange or spline interpolation, may be more appropriate in these situations.
Q) What are the advantages of using the Gauss backward interpolation formula?
Among the benefits are:
High precision for numbers close to the data set’s end.
Computing effectiveness for data points distributed uniformly.
the capacity to manage polynomials of higher order.
seamless changes in values between interpolated and known values.
Q) Are there any limitations to the Gauss backward interpolation formula?
Indeed, the following are some of the limitations:
requirement for data points to be spaced equally.
possible intricacy for big data sets.
sensitivity to data inaccuracies, which may have an impact on accuracy.
Q) How does the value of u affect the interpolation?
The value of u is determined by calculating x – xn / h ascertains the point x location in relation to the most recent data point xn . It affects the interpolation formula’s weights for the backward differences. For accurate interpolation, u must be calculated correctly.
