Fitting a Curve of the Form y=ax^b Using the Least Square Method

Fitting a Curve of the Form y=ax^b Using the Least Square Method

Introduction:

In the realm of data analysis, understanding complex nonlinear relationships is crucial. Mathematical models play a vital role in capturing and interpreting such relationships accurately. Among various techniques, the least square method stands out as a robust framework for fitting curves to data points. This comprehensive guide explores the art and science of fitting a curve of the form y = ax^b using the least square method.

Understanding the Essence of the Least Squares Method:

The least square method is a powerful mathematical approach used to find the best-fitting curve by minimizing the sum of the squares of the differences between observed and predicted values. This method excels in handling nonlinear relationships where linear models fall short, offering precision and accuracy in curve fitting.

Exploring the Power Function y = ax^b:

The curve fitting process centers around the power function y = ax^b, where constants a and b determine the magnitude and curvature of the curve, respectively. This versatile form can effectively model a wide range of nonlinear relationships with elegance and flexibility.

Step-by-Step Approach to Curve Fitting:

  1. Define the Model: The first step involves defining the mathematical model, the power function y = ax^b, laying the foundation for our curve fitting journey.
  2. Calculate the Residuals: By computing the residuals, the differences between observed and predicted values, we pave the way for further analysis.
  3. Square the Residuals: Transforming obstacles into opportunities, squaring the residuals sets the stage for minimizing their collective impact.
  4. Minimize the Sum of Squared Residuals: Utilizing optimization techniques like gradient descent, we determine the values of a and b that result in the most fitting curve.
  5. Evaluate the Fit: Metrics such as R^2 and RMSE offer valuable insights into the model’s accuracy, guiding our quest for understanding.

Practical Example and Implementation:

To demonstrate the curve fitting process, consider a dataset with potential awaiting exploration. Using Python and the SciPy library, we define the model function, generate sample data, fit the curve using curve_fit function, and extract the parameters a and b. This practical example showcases the application of the least squares method in real-world data analysis scenarios.

Advantages of Least Square Method:

Practical Applications:

The Least Squares Method is a widely used curve fitting technique in various areas.

Conclusion:

As we conclude our journey into curve fitting with the least squares method, we recognize the power and potential hidden within our data. This method serves as a guiding beacon through the complexities of nonlinear relationships, enabling us to uncover insights and chart new frontiers in data science. By mastering the least squares method, we navigate the data landscape with precision and clarity, paving the way for discovery and enlightenment.

Question:

Fit a curve of the form y=axb in the least square sense to the following observation:

x

1

2

3

4

5

y

0.5

2

4.5

8

12.5

Fit a curve of the form y=axb in the least square sense to the following observation:

x

1

2

3

4

5

y

0.5

2

4.5

8

12.5

Solution:

 y = axb                     (Eq A)

Taking “log” on both sides

 log y = log axb

 log y = log a + b log x              (Eq 1)

     Y = A +bX                            (Eq 2)

On Compairing (Eq 1) and (Eq 2),

Y = log y

A = log a

X = log x

 

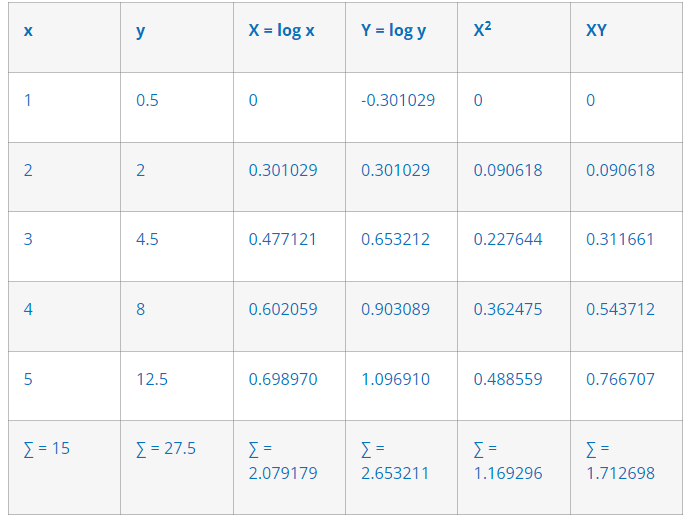
x

y

X = log x

Y = log y

X2

XY

1

0.5

0

-0.301029

0

0

2

2

0.301029

0.301029

0.090618

0.090618

3

4.5

0.477121

0.653212

0.227644

0.311661

4

8

0.602059

0.903089

0.362475

0.543712

5

12.5

0.698970

1.096910

0.488559

0.766707

∑ = 15

∑ = 27.5

∑ = 2.079179

∑ = 2.653211

∑ = 1.169296

∑ = 1.712698

The normal equations are

∑Y = nA + b∑X                    (Eq 3)

∑XY = A∑X + b∑X2              (Eq 4)

 

From (Eq 3)

2.653211 = 5A + 2.079179b

From (Eq 4)

1.712698 = 2.079179A + 1.169296b

5(Eq 4) – 2.079179(Eq 3)

8.56349 = 10.395895A + 5.84648b

5.51650 = 10.395895A + 4.32298b

3.04699 = 1.535b

b = 1.999993

b = 1.999993

Put in (Eq 3)

 

2.653211 = 5A + 2.079179(1.999993)

5A = -1.505132

A = -0.301026

 Also, A = log a

a = anti-log (A)

a = anti-log(-0.301026)

a = 0.500004

 

Put “a” and “b” in (Eq A)

y = axb

y = 0.500x1.999993

 

The normal equations are

∑Y = nA + b∑X                    (Eq 3)

∑XY = A∑X + b∑X2              (Eq 4)

 

From (Eq 3)

2.653211 = 5A + 2.079179b

From (Eq 4)

1.712698 = 2.079179A + 1.169296b

5(Eq 4) – 2.079179(Eq 3)

8.56349 = 10.395895A + 5.84648b

5.51650 = 10.395895A + 4.32298b

3.04699 = 1.535b

b = 1.999993

b = 1.999993

Put in (Eq 3)

 

2.653211 = 5A + 2.079179(1.999993)

5A = -1.505132

A = -0.301026

 Also, A = log a

a = anti-log (A)

a = anti-log(-0.301026)

a = 0.500004

 

Put “a” and “b” in (Eq A)

y = axb

y = 0.500x1.999993

 

Frequently Asked Questions (FAQs):

  Q) What is the least square method?

  By reducing the sum of squares of the discrepancies between the observed and predicted values, the least squares approach is a         mathematical technique that may be used to identify the curve that best fits a given set of data points.

  Q) What is the significance of fitting a curve of the form y = ax^b?

We can describe nonlinear interactions between variables by fitting a curve of the type y=ax^b. This provides a flexible framework for data analysis across a range of disciplines.

  Q) How does one use the least squares method to fit a curve?

By defining the model, calculating the residuals, squaring the residuals, minimizing the sum of squared residuals, and assessing the fit using the relevant metrics, one can fit a curve with the least squares approach.

  Q) What tools or libraries can I use to implement curve fitting in Python?

For curve fitting, Python provides a number of libraries, such as SciPy, NumPy, and Matplotlib. This flexible frame can viably demonstrate a wide run of nonlinear connections with class and adaptability.

  Q) Can the least squares method handle nonlinear relationships?

Indeed, the least square method works well with nonlinear interactions, which makes it a useful tool for fitting curves when linear models don’t match the data.

 Q) How do I interpret the parameters a and b in the curve y = ax^b?

The curve’s size or scale factor is represented by parameter 𝑎, while its curvature or shape is controlled by parameter b.

 Q) What metrics can I use to evaluate the fit of the curve to the data?

The root mean square error (RMSE), coefficient of determination (R2), and visual examination of the fitted curve in comparison to the data points are common metrics for assessing the fit.

 Q) Are there any limitations to the least squares method?

Although effective, the least square method could not always produce precise findings if the data contains outliers that materially affect the fit or if the underlying connection between the variables is extremely nonlinear.

Q) In what real-world scenarios is curve fitting using the least squares method commonly employed?

The least square method of curve fitting has applications in many disciplines, including biology, physics, engineering, finance, and economics, where it is crucial to comprehend and describe nonlinear interactions.

Q) Can I fit other types of curves using the least squares method?

Indeed, depending on the type of data and connection being represented, the least square method can fit a variety of curves, including polynomial, exponential, logarithmic, and power functions.