Fit a straight line using Method of Moments.
Introduction:
The Method of Moments is a tried-and-true method in statistics and data analysis that offers a solid framework for parameter estimate. Among its many uses, fitting a straight line to a dataset stands out as a fundamental activity that is crucial to industries ranging from physics to economics. The process and complexities of using the process of Moments to fit a straight line are explained in this article, along with the importance and usefulness of this approach for statistical inference.
Understanding the Method of Moments:
It is essential to grasp the fundamentals of the Method of Moments before diving into the details of fitting a straight line. Fundamentally, this approach is based on comparing empirical moments taken from the data with theoretical moments of a probability distribution. Robust statistical inference is made possible by deriving estimators for the parameters of interest by equating these moments.
Fitting a Straight Line:
Finding the Slope and Intercept that Best Describe the Relationship between Two Variables is the First Step in Fitting a Straight Line to a Dataset. This is using the first and second moments of the data distribution in the context of the Method of Moments.
The central tendency is captured by the first instant, which is the dataset mean, represented by the symbol μ. This means that for a straight line, the mean of the fitted line is equal to the mean of the observed y-values (the dependent variable).
Solving for Parameters:
Finding the Parameters:
The parameters of the straight line (𝛽0 and 𝛽 1) can be found using the system of equations generated from the moments. In order to separate the parameters and express them in terms of the dataset’s moments, this usually entails algebraic manipulation. The fitted straight line can then be obtained by computing these parameter estimators with the help of the observed sample moments.
Though the Method of Moments offers a strong foundation for fitting a straight line, there are several practical issues that should be taken into account. To guarantee the validity of the inference, it is first necessary to validate the underlying assumptions of the approach, such as the linearity of the relationship and the normalcy of the mistakes.
Furthermore, there are variants of the technique that can handle intricacies like heteroscedasticity or anomalies, enhancing its suitability in various contexts.
Moreover, the Method of Moments finds application in fitting more complex models and distributions, going beyond the domain of straight lines. Because of its simplicity and adaptability, it is a fundamental tool for statistical analysis, enabling practitioners and researchers in a variety of fields.
Applications
Using the Method of Moments to fit a straight line has the following applications:
Finance and Economics:
In economics, the Method of Moments can be used to fit a straight line and describe correlations between variables like GDP and consumption spending, supply and demand, or unemployment and inflation. This makes policy analysis and economic forecasting easier.
It can be applied to finance to help with risk management and investment decision-making by analyzing the relationship between stock prices and market indices, interest rates and bond yields, or firm income and advertising expenditure.
Physics and engineering:
In systems engineering, process control, and quality control procedures, the relationship between input and output variables can be analyzed using straight-line fitting. It can assist in comprehending, for instance, how temperature and pressure relate to one another in a thermodynamic system.
It can be used in physics to simulate various physical events, including the trajectory of a projectile, the relationship between voltage and current in Ohm’s law, and the relationship between force and displacement in Hooke’s law.
Social Sciences:
Straight-line fitting is a useful tool in sociology and psychology to examine correlations between variables like wealth and education level, crime rates and demographic characteristics, or happiness and social interactions.
In demography, it can be used to examine trends and dynamics in society by analyzing population growth rates, migration patterns, or fertility rates across time.
Environmental science:
It can be applied to environmental science to help with environmental monitoring and management by analyzing the relationship between environmental variables like temperature and precipitation, pollutant concentration and emission levels, or biodiversity and habitat characteristics.
Market Research and Consumer Behavior:
Straight-line fitting can be used in market research to examine the relationship between sales income, price elasticity of demand, or customer satisfaction ratings and marketing initiatives (such as advertising expenditure).
It can assist in understanding the relationship between demographic characteristics and purchase intention, brand loyalty and marketing campaigns, or product qualities and consumer preferences in consumer behavior analysis.
Conclusion:
Fitting a straight line with the Method of Moments is, in essence, the perfect example of how theory and practice in statistical inference may be combined. Through the utilization of the data distribution’s moments, this approach provides accurate parameter estimators that clarify the fundamental link between variables. The Method of Moments provides a reliable means of shedding light on patterns and phenomena included in datasets, especially as the field of data analysis expands.
Question:
Use method of moments to fit a straight line to the data given below:
|
x |
1 |
3 |
5 |
7 |
9 |
|
y |
1.5 |
2.8 |
4.0 |
4.7 |
6.0 |
Use method of moments to fit a straight line to the data given below:
|
x |
1 |
3 |
5 |
7 |
9 |
|
y |
1.5 |
2.8 |
4.0 |
4.7 |
6.0 |
Solution:
y = a + b x……………….. (1)
Since there are two unknowns,
So,
µ1 = r1 …………….. (2)
µ2 = r2……………… (3)
x |
y |
x y |
|
1 |
1.5 |
1.5 |
|
3 |
2.8 |
8.4 |
|
5 |
4.0 |
20 |
|
7 |
4.7 |
32.9 |
|
9 |
6.0 |
54 |
|
∑ = 25 |
∑ = 19 |
∑ = 116.8 |
And here h = 2
µ1 = h ∑y = 2 (19) = 38
µ2 = h ∑ x y = 2 (116.8) = 233.6
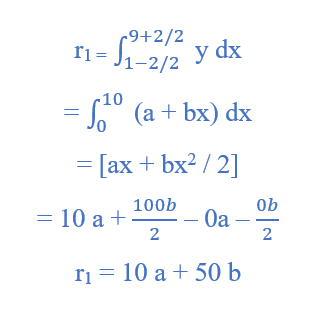

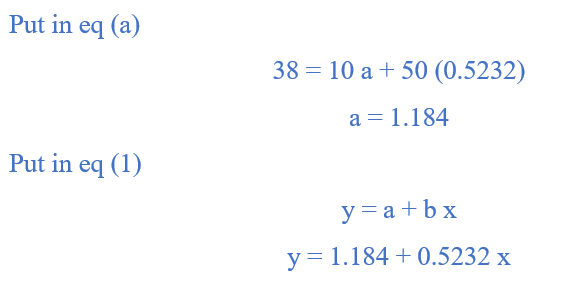
x |
y |
x y |
|
1 |
1.5 |
1.5 |
|
3 |
2.8 |
8.4 |
|
5 |
4.0 |
20 |
|
7 |
4.7 |
32.9 |
|
9 |
6.0 |
54 |
|
∑ = 25 |
∑ = 19 |
∑ = 116.8 |
And here h = 2
µ1 = h ∑y = 2 (19) = 38
µ2 = h ∑ x y = 2 (116.8) = 233.6
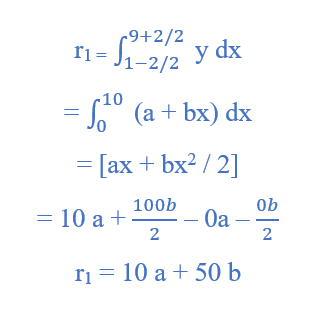

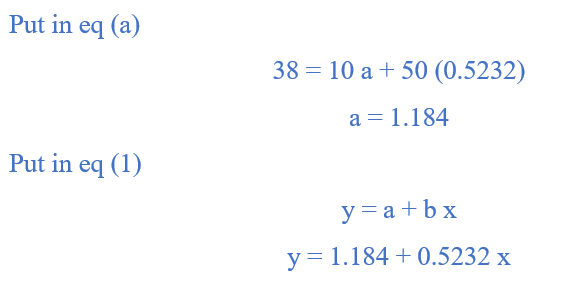
Frequently Asked Questions (FAQs):
What is the Method of Moments (MoM) in statistics?
For the statistical purpose of estimating parameters, the Method of Moments is employed. To estimate the parameters, theoretical moments of a probability distribution are equated with empirical moments obtained from observed data.
Why is fitting a straight line important in statistics?
We can represent and comprehend the link between two variables by fitting a straight line. It is essential for predictive modeling and inference in a number of disciplines, including the social sciences, physics, and economics.
How does the Method of Moments work for fitting a straight line?
By matching the first and second moments of the observed data distribution with the corresponding moments of the theoretical straight line, the Method of Moments fits a straight line. Estimators for the line’s intercept and slope can be found by solving these equations.
What are the assumptions underlying the Method of Moments for fitting a straight line?
The errors are assumed to be normally distributed with constant variance and to have a linear relationship between the variables according to the Method of Moments. It also presumes that each data point has an identical distribution and is independent.
What if the assumptions of the Method of Moments are violated?
Assumption violations may have an impact on the inference’s validity. In certain situations, different approaches or modifications might be required. For example, robust regression approaches can be used in the event of heteroscedasticity (unequal variance).
Can the Method of Moments be applied to nonlinear relationships?
The Method of Moments can be extended to nonlinear relationships by changing the variables or applying nonlinear regression techniques, even though it is usually used for linear models like fitting straight lines.
Is the Method of Moments the only method for fitting straight lines?
No, there are other techniques such as Bayesian estimating, maximum likelihood estimation, and the least squares method. The model’s assumptions and the type of data are two examples of variables that influence the method chosen.
How do I validate the results obtained from the Method of Moments?
Verifying if the fitted model accurately depicts the data is the process of validation. This can be accomplished by looking at residual plots, testing hypotheses, and evaluating goodness-of-fit metrics such as R-squared.
What are the advantages of using the Method of Moments for fitting a straight line?
Iterative optimization is not necessary when using the Method of Moments, and its implementation is quite straightforward. It is computationally efficient as well because it offers parameter estimator closed-form answers.
Where can I learn more about the Method of Moments and its applications?
The Method of Moments and its applications in statistics and data analysis are covered in a wide range of textbooks, online courses, and scholarly materials. Furthermore, attending workshops or speaking with statisticians might provide insightful advice.
