Fit a parabola of the form y = ax^2+bx+c

Fit a parabola of the form y = ax^2+bx+c

Understanding and Using the Form y = ax^2 + bx + c
:

Parabolas are common curves in mathematics and physics that are used to explain a variety of natural and artificial events. They can be found, among other things, in statistical modeling, engineering designs, optics, and projectile motion. The quadratic equation in standard form is one of the most widely used representations of a parabola:

y = ax² + bx  + c

The shape, orientation, and position of the curve are determined by the constants 𝑎a, 𝑏b, and 𝑐c, which together represent the fundamental properties of a parabola. This essay will examine how to fit parabolic data using this form, comprehend its graphical representation, and delve into real-world applications in a variety of academic fields.

Understanding the Components of y=ax^2+bx+c:

Coefficients a, b, and c:

 

Graphical Representation:

The graph of y=ax 2 + bx + c is a smooth, U-shaped curve known as a parabola. Its position in the coordinate plane is dictated by b and c, and its concavity (upward or downward) is dependent on the sign of a.

Fitting a Parabola to Data:

Fitting a parabola to a collection of data points is a standard practice in many scientific and engineering applications. The steps in this procedure are to determine which values of A, B, and C most closely resemble the provided data. This is how it’s usually carried out:

Least Squares Method:

The least squares method is the most popular way to fit a parabola. It entails minimizing the sum of squared differences between the real data points (x i, y i) and the corresponding points on the parabola (ax i, +bx i, +c).

Matrix Formulation:

By using this technique, the issue is converted into a matrix equation.

Ax=y, in which

A is a coefficient matrix.

x is an unknown vector.

(a, b, c), and

y is an observed data vector.

 

Solver Algorithms:

The Gauss-Newton method, gradient descent, and polynomial regression approaches are a few examples of computational algorithms that can be used to solve for

a, b, as well as c effectively.

Applications Across Disciplines:

Projectile Motion: Because of gravitational acceleration, a projectile’s trajectory is parabolic.

Optics:  In optics, light is focused in telescopes, satellite dishes, and optical devices using parabolic mirrors and lenses.

Cost and Revenue Analysis: The profitability and optimization of businesses are examined using quadratic cost and revenue functions.

Population Growth: Time-dependent population growth dynamics can be explained by parabolic models.

 

Curve Fitting: Utilized in data science regression analysis when a parabolic trend is suggested by the association between the variables.

Signal Processing: Signal peak levels are highly precisely estimated using parabolic interpolation.

Practical Example: Fitting a Parabola to Experimental Data

Consider carrying out an experiment in which you gauge the height of a ball thrown upward at various points in time t. The initial velocity and gravitational acceleration can be found by fitting the resultant data points to a parabolic equation. Through the use of

y=at^2+bt+c,

in which half of the gravitational acceleration is represented by a.
The initial velocity is related to b, and
C stands for the starting height.

 

Conclusion:

Not only is the equation y=ax^2+bx+c a mathematical abstraction, but it is also an effective tool for simulating real-world phenomena in a variety of domains. It is essential for theoretical study as well as real-world applications due to its adaptability in defining parabolic shapes and patterns. Deriving meaningful insights from data and events around us requires the ability to fit and comprehend parabolic equations, whether one is investigating projectile flight, streamlining corporate processes, or examining data trends.

Question:

Fit a parabola of the form y = ax2 + bx + c to the data:

 

x

1

2

3

4

y

1.7

1.8

2.3

3.2

Fit a parabola of the form y = ax2 + bx + c to the data:

 

x

1

2

3

4

y

1.7

1.8

2.3

3.2

Solution:

                               y = ax2 + bx + c……………. (1)

Since, there are three unknowns

So,

        µ1 = r1

        µ2 = r2

        µ3 = r3

x

y

x y

x2

x2 y

1

1.7

1.7

1

1.7

2

1.8

3.6

4

7.2

3

2.3

6.9

9

20.7

4

3.2

12.8

16

51.2

∑ = 10

∑ = 09

∑ = 25

∑ = 30

∑ = 80.8

And here h = 1

       µ1 = h ∑y = 1 (9) = 9

       µ2 = h ∑xy = 1 (25) = 25

       µ3 = h ∑x2 y = 1 (80.8) = 80.8

Limit of integration (1 – 1 / 2, 4 + 1 / 2)

                                 (0.5, 4.5)

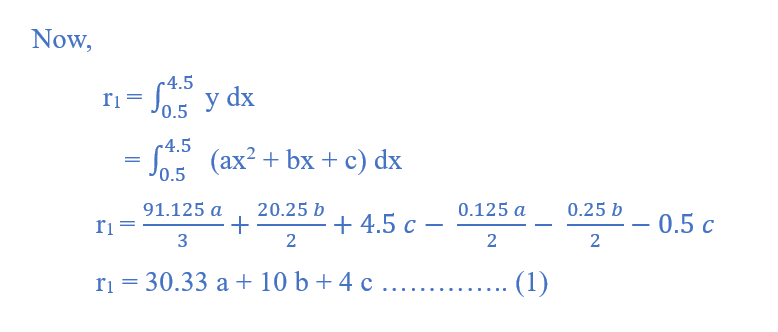
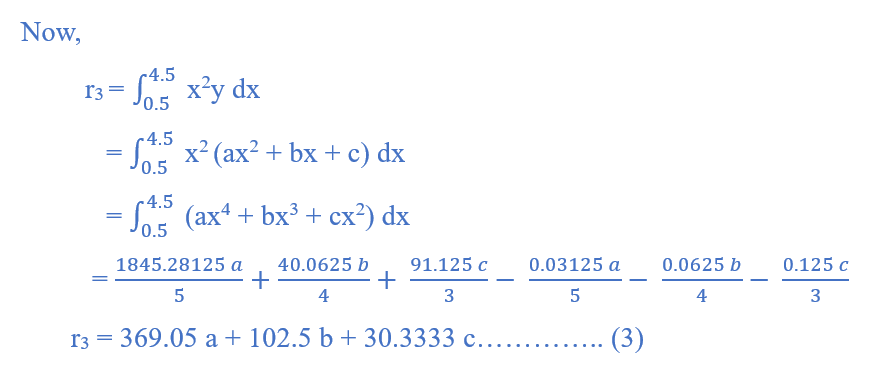
Put a, b, c in equation (1)

                            y = ax2 + bx + c

                            y = 0.008 x2 + 0.4248 x + 1.1213

x

y

x y

x2

x2 y

1

1.7

1.7

1

1.7

2

1.8

3.6

4

7.2

3

2.3

6.9

9

20.7

4

3.2

12.8

16

51.2

∑ = 10

∑ = 09

∑ = 25

∑ = 30

∑ = 80.8

And here h = 1

       µ1 = h ∑y = 1 (9) = 9

       µ2 = h ∑xy = 1 (25) = 25

       µ3 = h ∑x2 y = 1 (80.8) = 80.8

Limit of integration (1 – 1 / 2, 4 + 1 / 2)

                                 (0.5, 4.5)

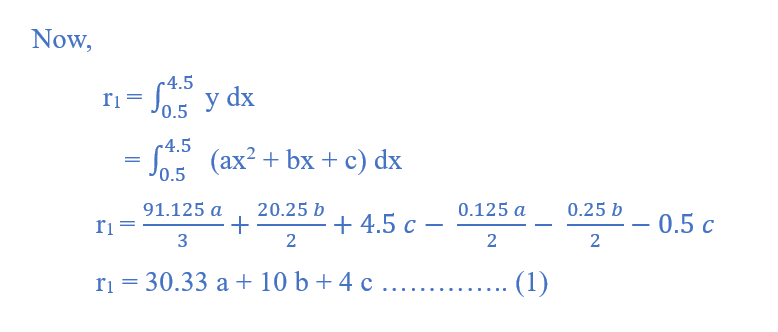
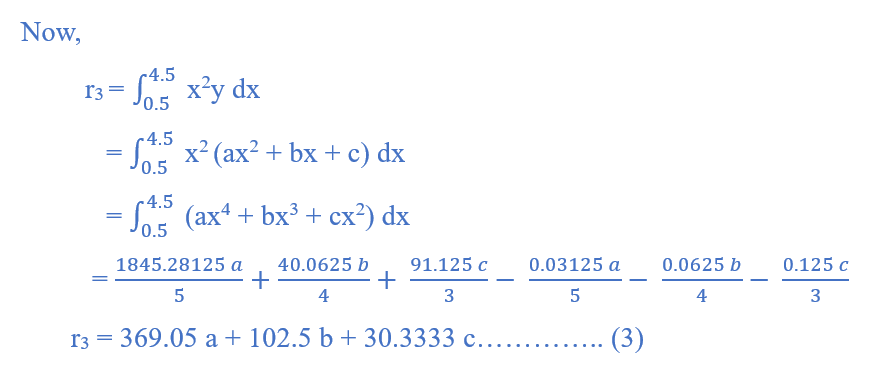
Put a, b, c in equation (1)

                            y = ax2 + bx + c

                            y = 0.008 x2 + 0.4248 x + 1.1213

Frequently Asked Questions (FAQs):

Q) What is a parabola and why is y=ax2+bx+cy = ax^2 + bx + c important?

The quadratic equation y=ax^2+bx+c, where a, b, and c are constants, defines a parabola as a U-shaped curve. This form is important because it provides a very accurate description of many real-world phenomena, such as projectile motion, optics, and economic modeling.

Q) How do you interpret the coefficients a, b, and c in y = ax^2 + bx + c?

a: Establishes the parabola’s direction and form. Negative an opens downward, and positive an opens upward.
b: Affects the parabola’s symmetry and horizontal shift, or the vertex’s location.
c: Depicts the point on the y-axis where the parabola crosses the y-intercept.

Q) What methods are used to fit a parabola to data?

The least square method, which minimizes the sum of squared discrepancies between actual data points and corresponding values predicted by y=ax^2+bx+c, is the most widely used methodology. For effective computing, matrix formulations and solver algorithms such as Gauss-Newton or gradient descent are also used.

Q) In which fields and applications is the parabola y = ax^2 + bx + c used?

Many applications of parametric equations include:

Physics (such as optics and projectile motion)
Engineering (such as signal processing and structural design)
Economics (such as revenue optimization and cost analysis)
Data science, including statistical modeling and curve fitting

Q) Can y=ax2+bx+cy = ax^2 + bx + cy=ax2+bx+c represent both upward and downward opening parabolas?

Yes, depending on the sign of a:

Q) How is y = ax^2 + bx + c applied in practical scenarios?

It is employed to model and examine a range of phenomena:

projectile trajectory prediction.
optically designing reflective surfaces.
examining the income and cost functions in business.
curve fitting for data analysis and scientific study.

Q) How accurate is fitting a parabola y=ax2+bx+cy = ax^2 + bx + cy=ax2+bx+c to real-world data?

Proper fitting of parabolic equations using strong techniques such as least squares can yield very accurate representations of a wide range of statistical, economic, and physical phenomena. The appropriateness of the selected model and the quantity and quality of the data determine accuracy.